Lithium-Ion drives the Future
The basic innovation LiIon battery, driven by the company Sony, has surprising, but that is common in innovation, enabled the development of electric cars.
Previously there were only ugly batteries, some were extremely heavy, lead-acid battery, extremely toxic, nickel cadmium, or other drawbacks why they were not suitable for an energy storage device in a car. This has seduced the automotive industry to believe everything would stay the same and no special attention was given to the development of batteries.
With the successful development of the Tesla S, an all-electric car, everything has changed fundamentally, so I will report here about the importance of battery technology in the automotive industry.
The value Chain in the Car Industry (today)
Four things make the value of a car:
- the glider, a vehicle without powertrain and energy storage
- the engine with storage (tank or battery)
- the image of the brand (mostly through advertising)
- the amount of energy consumed by the car in his life
The glider is now a product of the OEM, headlights, bumper, seats or wheels and tires, almost everything visible to the driver is not produced in the car factory. Only the steel welding of the body remains in most car factories, with high automation done by robots.
The engine remains us to the 19th century. An internal combustion engine with a mean efficiency of about 20 percent, emitting significant amounts of particulate matter and other unhealthy substances, accelerates the car more or less rapidly to cruising speed and keeps on this pace. Thousands of engineers try to optimize this technology with legal or illegal means.
The image of cars of different brands developed by massive advertising budgets [1]. Through product placement in movies and elaborate sales centers, a high value of the car is suggested, although all the cars stuck in traffic driving at the same speed. For many people, the car is next to the house, the most expensive product that is purchased for own appreciation.
The fuel that a car burns during its operational phase of approximately 200,000 miles (ca. 321,869 km), may sum up to $30,000 (depending on local tax) and is often more expensive as the whole car. In addition, no one knows during car purchase how the gas price will develop. The money ends up in the pockets of the oil companies and oil states, not in the automotive industry!
Summarized, the major carmakers only can manufacture engines, the rest of the value chain is lost.
The electric car value chain
Electric cars have a significantly different distribution to the above points 1 to 4
The glider remains essentially the same, interestingly, the weight saving is less important than with previous cars because by recuperation (recovery of braking energy). The energy to accelerate and the energy to go uphill is not used for heating the brake disk, as in conventional cars.
The use of non-rusting aluminum is useful because the life of an electric motor is considerably higher than that of an internal combustion engine. And who wants a rusty electric car that still has a good engine and a working battery.
The value of the electric motor is far below of an internal combustion engine, which consists of 6000 moving precision parts. Electric motors are simple, some copper wire winding and an aluminum cylinder which rotates. Rare earth elements are not necessary, which can only be found in hybrid cars like the Toyota Prius (46 kg!).
There is no fuel in the electric car. But we need a battery and electric power to drive the car. The batteries are by far the most expensive part in an electric car and remarkably similar in price compared to the fuel costs of a conventional car.
Amazingly, this was not noticed neither by the big oil companies nor the major car companies. Exception: Tesla builds a Gigafactory, a battery factory which can supply batteries for about 500,000 electric cars a year, thus making the company independent from other suppliers.
Only the German company Volkswagen has announced that it is considering $ 11.000.000.000 to invest in the construction of a battery company (
GAS2) Unfortunately, I have heard such announcements in the area of e-mobility by automotive companies several times. Actual, so far nothing was created.
The "fuel" power would actually be a clear claim for the utilities or oil companies. Here there is complete silence.
The problem of everyday usefulness
If you want to use an electric car just like your previous car, it must be reliable cover about 60 miles a day, but it has also to master the holiday trip or extended business trips.
For daily demand, the socket in the garage is sufficient for overnight charging. resulting in a very limited contact to a gas station. Except perhaps refill the windshield wiper fluid and visit the car wash.
On longer trips, every car must refuel new energy. At the gas station, this is done within five minutes. To charge an electric car during the trip should not substantially extend the duration of the trip. So it is imperative that there is a network of fast-charging stations.
At this point, I'm amazed to read that the policy in Germany will subsidize 10,000 charging stations (per charging station $ 70.000 tax money). However, they do not demand the fast charging ability.
Only charging stations, where you can charge more than 200 miles range in 30 minutes (supercharger) lead to everyday practicality of electric cars.
No other company than Tesla operates or plans to operate a supercharger network. A network that could be owned by an automaker or other organization. I think oil companies, motorway service areas or power companies, should be interested to roll out a fast charging network,
Ending up in a monopoly situation, anyone who is interested in an everyday useful car can now only buy a car from Tesla, all other manufacturers have virtually no usable electric car on offer.
The fairytale "battery problem"
The common theme in the discussion about electric cars is the battery problem. It involves at least three subjects
- battery price
- lifespan
- raw materials
Prices of batteries are in free fall. On the picture, you can see a slide that has been shown on the Menasol 2016 Energy Conference in Dubai. Compared to the drop in solar cell price, the price of LiIon batteries appears to move even more quickly down.
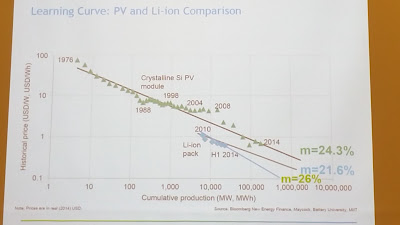 |
| Development of battery prices, when the market doubles the volume, the price drops by 26% |
If the price of batteries is at $250 per kWh and a car needs for the daily use about 80 kWh, the battery will cost $20,000. Counting the cost of electricity results in less than the fuel costs of a conventional car.
The service life for batteries depends on the charging cycles, and some other factors, such as temperature decreases. A Thousand charging cycles required can be delivered by virtually all the batteries, even a lead battery. But this means 200,000 miles (1,000 times 200 miles per charge) is easily reachable by a battery and beyond the lifespan of the vehicles. Moreover, it seems to be that although there is a slight decrease in capacity, a second life of the battery is possible. For example, to use the battery in a PV system for overnight storage.
The raw material lithium (60ppm [2]) is much more common than lead (18 ppm in the earth's crust [3]) to be found. Thus, there is no problem of raw materials, even if it could lead to bottlenecks due to slow expansion of mining activity. Unlike oil, lithium is not consumed in the car but can be 100% reused. Lithium is also non-toxic, who spices his soup with sea salt, is eating lithium salt, which in large quantities is part of the sea(salt).
Old industry fails in innovation
Although the facts about electric cars are easy to understand, you wonder why the auto industry is doing almost nothing. The problem is more than a century of grown structures. Virtually all automakers are over 100 years old, except for Volkswagen, a company which was established on 28 May 1937 by Hitler.
In these companies, there is extremely much knowledge about internal combustion engines. Ignition and oxygen supply, exhaust and catalyst are investigated by expensive and complex means. The technological elite in the automotive industry understands the combustion engine, studied and graduated on that topic.
Battery technology, lithium-ion, and electrolytes they have heard about in the media. It is not their core competency. How to go about developing the technology? The natural reaction is waiting and building seven-speed transmission and hybrid engines or even worse hydrogen engines.
Simultaneously a startup, Tesla Motors, succeeded to be about five years ahead of the pack. Installed thousands of supercharger stations and without expensive advertising build a brand image that fits a clean environment with renewable energy.
It would not be new in the history of innovation that industry does not survive the change in technology. No sailing Shipyard has built steamboats, short before bankruptcy they tried with seven master sail and "hybrid" (Sail plus steam engine).
No mail order retailer could defeat Amazon or eBay.
No telephone company, Siemens, Motorola nor Nokia, plays an important role in the smartphone league.
We will have to accept that some companies like VW / BMW / Daimler are in ten years only a brand name but no longer large employers.
Peter Schumpeter described this with the words
"Creative destruction"
And he probably has once again right.
Further comments:
[1] Volkswagen spent more than $110 million in Germany for advertising in the months January till April 2016, source: Nielsen /
Statista.
[2] ppm stands for "parts per million", which means you take a ton of average rock, then 60 grams of lithium and 18 grams of lead are contained therein.
[3] The mass fraction concealed, that a kg of lead can only store about a factor of 50 less energy than a kg of lithium. Viewed from this condition, you need less lithium for all cars (if they are electric) than lead is used today for starter batteries in petrol and diesel cars.